Magic Square
In mathematics - particularly in recreational and historical contexts - a magic square is a square grid of numbers arranged so that the sum of the numbers in each row, column, and both main diagonals is the same. This sum is called the magic constant.
A magic square of order n contains n² numbers arranged in an n × n grid. If the square uses all the integers from 1 to n² exactly once, it is known as a normal magic square. In some cases, the term "magic square" is used specifically to refer to this normal form.
Magic squares have intrigued mathematicians for centuries and have also appeared in art, architecture, and mysticism. Variants include arrangements using different sets of numbers or even letters, sometimes referred to as word squares.
Normal Magic Squares and Their Properties
A normal magic square of order n is an n × n grid filled with the distinct integers from 1 to n², arranged in such a way that the sums of the numbers in every row, every column, and both main diagonals are equal. This shared total is known as the magic constant or magic sum, commonly denoted by M.
Existence and the Smallest Case
Normal magic squares exist for all orders n ≥ 1, with the exception of n = 2, for which no such arrangement is possible. The case n = 1 is considered trivial, as it consists of a single cell containing the number 1 and thus trivially satisfies the condition.
The smallest nontrivial example of a normal magic square is of order 3:
image of the 3×3 magic square
The Magic Constant
The magic constant M for a normal magic square depends only on the order n and is given by the formula:
M = n(n² + 1) / 2
Using this formula, the magic constants for the first few orders are:
- n = 3: M = 15
- n = 4: M = 34
- n = 5: M = 65
- n = 6: M = 111
- n = 7: M = 175
- n = 8: M = 260
These values form a sequence known in the On-Line Encyclopedia of Integer Sequences (OEIS) as A006003.
Variants: Trivial and Semimagic Squares
Not all arrangements that resemble magic squares meet the strict definition of a normal magic square. In particular:
- Trivial magic squares may include repeated numbers or deviate from the requirement of using all integers from 1 to n². Some well-known examples, such as the Sagrada Família magic square and the Parker square, fall into this category.
- A semimagic square (also known as an orthomagic square) is one in which all rows and columns sum to the magic constant, but the diagonals do not necessarily do so. While related, these are not considered true magic squares under the standard definition.
A Brief History of Magic Squares
Magic squares have a rich and fascinating history that stretches back thousands of years. Long before the rise of classical civilizations like the Greeks, Romans, or Hebrews, magic squares appeared in ancient China, where they were imbued with mystical and symbolic meaning.
Ancient Origins in China
One of the earliest known references to a magic square dates to around 2200 BCE in ancient China. According to legend, the mythical Emperor Yu the Great witnessed a remarkable event: a turtle emerged from the Lo River, bearing strange markings on its shell. These markings formed a square arrangement of numbers which, when summed horizontally, vertically, or diagonally, all produced the same total. This square, known as the Lo Shu Square, became an object of mathematical curiosity and spiritual reverence, laying the foundation for what we now call magic squares.
The earliest written reference to magic squares is found in the works of Zhuang Zi, a Daoist philosopher from the 4th century BCE, further evidencing their long-standing place in Chinese intellectual culture.
Transmission to the Islamic World
Magic squares later spread westward. By the 7th century CE, Arab scholars had begun to engage with Indian mathematical traditions following the Islamic conquests of parts of the Indian subcontinent. Through this cultural exchange, they encountered magic squares along with other concepts in astronomy, arithmetic, and combinatorics.
The first known magic squares of orders 5 and 6 appear in the 10th-century encyclopedic work Rasa’il Ikhwan al-Safa (The Epistles of the Brethren of Purity), compiled in Baghdad around 983 CE. Earlier Arab mathematicians had already studied simpler squares, and over time, these mathematical objects found their way into more esoteric uses. Notably, they were incorporated into occult texts such as Shams al-Maʿārif, where they were used alongside so-called magic letters by mystics and illusionists.
Occult Symbolism and Artistic Influence
Over the centuries, magic squares came to be associated with mysticism, astrology, and alchemy in various cultures. Their appearance in art and architecture - often as symbols of cosmic harmony or protective talismans - underscores their enduring symbolic power. The most famous example is the Sagrada Família magic square, incorporated into the facade of Gaudí’s basilica in Barcelona.
Modern Interpretations and Extensions
In contemporary mathematics, magic squares continue to inspire exploration and generalization. Researchers have extended the concept in various directions:
- Using different operations, such as multiplication instead of addition.
- Applying the idea to alternative shapes or higher dimensions (e.g., magic cubes).
- Replacing numbers with symbols, geometric figures, or matrices, allowing for a variety of algebraic and visual interpretations.
While once regarded as mystical, magic squares today are appreciated as elegant objects of recreational mathematics, blending logic, pattern, and historical depth.
The Lo Shu Square: China's Ancient 3×3 Magic Square
The Lo Shu Square (洛書, Luòshū) is the earliest known example of a normal magic square of order 3. Originating in ancient China, this 3×3 grid of numbers has been revered for millennia, not only for its mathematical properties but also for its profound cultural and cosmological significance. It has influenced various aspects of Chinese thought, including philosophy, astronomy, numerology, and geomancy.
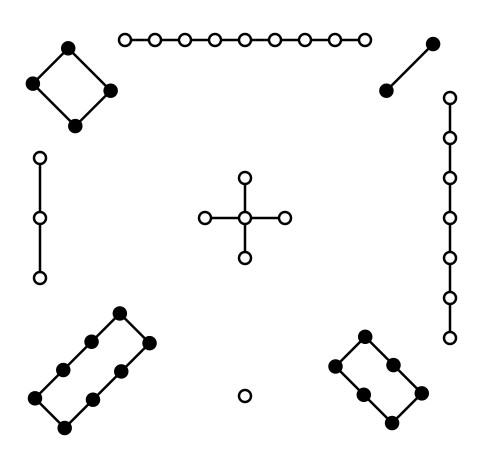
The traditional Luoshu diagram. (source: commons.wikimedia.org)
Mythical Origins: The Turtle of the Luo River
According to ancient Chinese legend, during the reign of the mythical Emperor Yu the Great (circa 2200 BCE), a great flood threatened the land. As Emperor Yu attempted to control the deluge, a divine turtle emerged from the Luo River (洛河), bearing a curious pattern of dots on its shell. These dots formed a 3×3 grid where the numbers 1 through 9 were arranged such that the sum of each row, column, and diagonal equaled 15. This pattern was interpreted as a heavenly message, guiding Emperor Yu in his flood control efforts and symbolizing cosmic harmony.
Historical References and Cultural Influence
The earliest textual reference to the Lo Shu Square appears in the writings of Zhuang Zi (369–286 BCE), a foundational Daoist philosopher . Over time, the Lo Shu Square became intertwined with various aspects of Chinese culture:
- Philosophy and Cosmology: The square was associated with the Five Elements (五行, Wǔxíng) and the Eight Trigrams (八卦, Bāguà), foundational concepts in Chinese metaphysics.
- Urban Planning: Ancient Chinese city layouts often reflected the Lo Shu's symmetry, emphasizing balance and harmony .
- Feng Shui: Practitioners used the Lo Shu Square to assess and harmonize the energy flow (qi) within spaces, influencing architectural and interior design decisions .
Structure and Properties of the Lo Shu Square
The Lo Shu Square is unique among 3×3 magic squares. Its standard configuration is:

The unique normal magic square of order 3, also known as the Lo Shu Square. (source: commons.wikimedia.org)
Key properties include:
- Magic Constant: Each row, column, and diagonal sums to 15.
- Symmetry: The square exhibits rotational and reflective symmetry.
- Numerical Balance: The central number is 5, and numbers opposite each other across the center sum to 10.
These characteristics symbolize balance and harmony, reinforcing the square's significance in various cultural contexts.
Illustrations and Visual Representations
Visual depictions of the Lo Shu Square often accompany the legend of the turtle from the Luo River. Traditional illustrations showcase the turtle with the 3×3 grid on its shell, emphasizing the square's divine origin. Such imagery reinforces the square's mystical and cosmological associations.
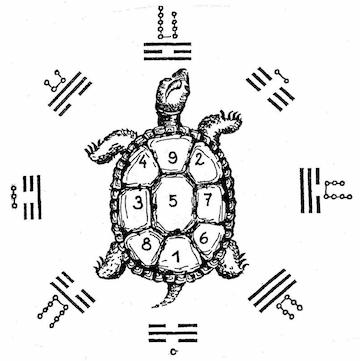
Turtle triads from left to right and from head to tail. (source: proza.ru)
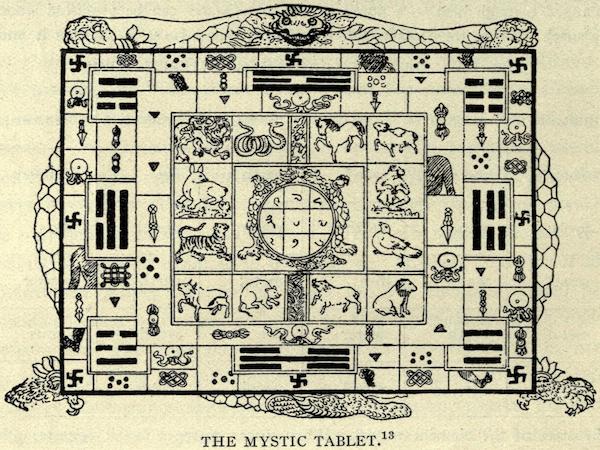
The Lo Shu square on the back of a small turtle (in the center), surrounded by the signs of the Chinese zodiac and the Eight Trigrams, are all carried by a large turtle (that presumably stands for the Dragon horse that had earlier revealed the trigrams to Fu Xi). This example drawn by an anonymous Tibetan artist. (source: commons.wikimedia.org)
Legacy and Modern Relevance
The Lo Shu Square's influence persists in contemporary practices:
- Mathematics: It serves as an introduction to magic squares and combinatorial designs.
- Feng Shui: Modern practitioners continue to use the Lo Shu Square to analyze and optimize spatial energy flows.
- Cultural Symbolism: The square remains a symbol of balance, harmony, and cosmic order in various artistic and philosophical contexts.
Magic Squares in Persian Tradition
The exact origins of magic squares remain uncertain, and scholars continue to debate their earliest appearances. While magic squares are often associated with Chinese antiquity, it has also been suggested that they may have independently developed in pre-Islamic Persia. Although definitive evidence for this hypothesis is lacking, the idea persists in historical discourse, particularly due to Persia's long-standing engagement with mathematics and numerology.
Medieval Persia and the Islamic Golden Age
Magic squares gained notable prominence in medieval Persian mathematics, particularly during the Islamic Golden Age (8th to 13th centuries CE). The study of mathematical patterns and recreational number theory flourished in this era, alongside advancements in algebra, astronomy, and geometry.
One of the earliest documented Persian references to magic squares appears in the 10th century. The renowned Persian mathematician Abu al-Wafa' Buzjani (940–998 CE), known for his work in trigonometry and geometry, included magic squares in one of his manuscripts. On page 33 of the manuscript, Buzjani presents a series of magic squares constructed using arithmetic progressions. Each square is filled in such a way that the sums of the numbers in each row, column, and diagonal are equal - a defining feature of magic squares.

Buzjani, Persian mathematician and astronomer. (source: commons.wikimedia.org)
These early Persian contributions are considered some of the earliest Islamic examples of magic squares and show a continuity of mathematical curiosity that bridged earlier Hellenistic, Indian, and Chinese traditions. It is also notable that these developments occurred after the introduction of chess into Persia, a game which itself shares deep ties with numerical pattern recognition and strategy.
Cultural Significance and Influence
In Persian and broader Islamic contexts, magic squares were not just mathematical curiosities - they often carried mystical or talismanic significance. They were integrated into astrology, alchemy, and Islamic occult sciences (such as ilm al-huruf, or the science of letters). Later texts like Shams al-Ma'arif (The Sun of Knowledge) expanded on the use of magic squares in magical and esoteric practices.
Conclusion
While the precise origins of magic squares in Persia remain elusive, the region played a significant role in their mathematical development and cultural diffusion during the medieval period. Through scholars like Buzjani and others, Persia contributed to preserving and expanding the knowledge of magic squares, setting the stage for their continued study across both the Islamic world and Renaissance Europe.
Further reading and references:
- Berggren, J. L. Episodes in the Mathematics of Medieval Islam. Springer, 1986.
- Sesiano, Jacques. Islamic Mathematics. Edinburgh University Press, 2011.
- Dastur, F. (1992). The Historical Role of Persia in Mathematical Transmission. Journal of the History of Science in Iran.
The Development of Magic Squares in the Arab World
Magic squares, mathematical constructs where the sum of each row, column, and diagonal is identical, gained significant traction in the Islamic world during the medieval period. Their introduction to Arabic mathematical thought likely occurred as early as the 7th century, during the rapid expansion of the Islamic Caliphate.
Origins and Transmission
Arab scholars first encountered magic squares through cultural exchanges with India and possibly China. During the early Islamic conquests, particularly in regions such as the Indian subcontinent, Arab intellectuals assimilated and translated Indian texts on astronomy, mathematics, and astrology - fields in which the concept of ordered numerical patterns played a crucial role. Some historians also posit an independent Chinese influence, particularly through the Silk Road, where ideas such as the Lo Shu Square may have traveled westward ([Pingree, 2001]).
Early Islamic Texts and the Brethren of Purity
The earliest documented examples of higher-order magic squares (specifically orders 5 and 6) appear in the "Rasa'il Ikhwan al-Safa" (Epistles of the Brethren of Purity), an encyclopedic work compiled around 983 CE in Baghdad. This encyclopedic compendium, attributed to a secretive philosophical society, integrated Neoplatonic, Pythagorean, and Islamic concepts with mathematical and metaphysical studies. Within its pages, magic squares are presented not just as recreational curiosities but as objects of cosmic and symbolic importance.
Before this, simpler magic squares of lower orders (such as 3×3 and 4×4) were already circulating among Arab mathematicians. These early versions may have served both mathematical and mystical purposes, paving the way for later elaborations.

Double-leaf frontispiece from the "Encyclopedia of the Brethren of Purity". Baghdad, 1287. Süleymaniye Library (MSS Esad Efendi 3636). (source: commons.wikimedia.org)
Ahmad al-Buni and Mystical Interpretations
One of the most prominent figures in the esoteric application of magic squares was the 13th-century mathematician and mystic Ahmad al-Buni (d. c. 1225). Best known for his influential work Shams al-Ma'arif al-Kubra ("The Sun of Great Knowledge"), al-Buni explored the mystical properties of letters and numbers, embedding magic squares within numerological and talismanic practices.
Although al-Buni did not detail the precise mechanisms of the magical powers he attributed to magic squares, his work suggests they were used in astrological calculations and protective charms. These squares were often inscribed on amulets, manuscripts, and architectural elements, reflecting their role in Islamic occult sciences (‘ilm al-huruf and ‘ilm al-awfaq).
Cultural Impact and Legacy
By the late medieval period, the study of magic squares in the Islamic world had evolved into a sophisticated branch of both recreational mathematics and esoteric science. From Baghdad to Cairo and Andalusia, Islamic scholars integrated magic squares into diverse disciplines - ranging from astronomy to mysticism - ultimately influencing European Renaissance thinkers through translations of Arabic texts.
Further reading and references:
- Pingree, David. The Thousands of Abu Maʿshar. Brill, 2001.
- Nasr, Seyyed Hossein. Science and Civilization in Islam. Harvard University Press, 1968.
- Dhanani, Alnoor. The Physical Theory of Kalām: Atoms, Space, and Void in Basrian Mu'tazilī Cosmology. Brill, 1994.
- Savage-Smith, Emilie. Magic and Divination in Early Islam. Ashgate/Variorum, 2004.
Magic Squares in Indian Tradition
India has one of the oldest known traditions of magic squares, with roots stretching back to Vedic times. These squares were not merely mathematical curiosities but served ritualistic, spiritual, and symbolic purposes in Hinduism, Jainism, and related Indic traditions. Among the oldest forms is the 3×3 magic square, which remains in use today in yantras - mystical diagrams employed in meditative and religious practices.
The Ganesh Yantra
One of the most prominent examples is the Ganesh Yantra, a 3×3 magic square associated with the Hindu god Ganesha, the remover of obstacles. In this square, the numbers are arranged so that all rows, columns, and diagonals sum to the same constant. The symmetry and balance of the square are believed to embody spiritual harmony and cosmic order, making it a powerful talisman in devotional settings.

Ganesh Yantra (source: shaligram.com)
The Chautisa Yantra: India’s 4×4 Magic Square
A more elaborate early example of a magic square is the Chautisa Yantra, a 4×4 square prominently displayed in the Parshvanath Jain Temple at Khajuraho, dated to the 10th century CE. The name Chautisa derives from the number 34, which is the magic constant of this square - each row, column, and both main diagonals all sum to 34.

Chautisa Yantra (source: commons.wikimedia.org)
Chautisa Yantra (Khajuraho, 10th century)
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
This magic square displays remarkable mathematical richness. In addition to the standard properties, it exhibits the following advanced symmetries:
- All 2×2 subsquares sum to 34.
- The corners of the 3×3 and 4×4 sections each total 34.
- Certain diagonally symmetric groupings, such as (1+11+16+6) and (2+12+15+5), also yield the same sum.
- The middle entries of the outer rows and columns (12+1+6+15 and 2+16+11+5) each add up to 34.
These features elevate the Chautisa Yantra beyond a simple arithmetic structure, suggesting deliberate design for mystical and symbolic significance - a quality that mirrors the square’s sacred placement within the Jain temple architecture.
Cultural and Religious Significance
Magic squares in Indian culture have often been closely linked to yantric diagrams, astrological charts, and cosmic symbolism. The recurrence of specific numerical patterns was thought to reflect cosmic rhythms, and their construction was regarded as a form of sacred geometry. Whether inscribed on metal plates, engraved in temples, or used in rituals, magic squares like the Chautisa Yantra represent the intersection of mathematics, cosmology, and spirituality in ancient Indian thought.
Further reading and references:
- Kak, S. (2001). Indian Mathematics and Astronomy: Some Contemporary Research. Center for Indic Studies.
- Sarma, K.V. (1992). A History of the Kerala School of Hindu Astronomy. Vishveshvaranand Institute.
- Datta, B. & Singh, A. N. (1935). History of Hindu Mathematics. University of Calcutta Press.
- Pingree, David. (1981). Jyotiḥśāstra: Astral and Mathematical Literature. Otto Harrassowitz Verlag.
Magic Squares in Europe: From Mathematical Curiosities to Mystical Symbols
Magic squares - grids where numbers are arranged so that the sums of each row, column, and diagonal are equal - have captivated minds across cultures and centuries. In Europe, their journey began as mathematical explorations and evolved into tools of mysticism and art.
Manuel Moschopoulos: Introducing Magic Squares to the West
Around 1300 CE, Greek Byzantine scholar Manuel Moschopoulos authored a treatise on magic squares, marking the first known Western work on the subject. Departing from the mystical interpretations of his predecessors, Moschopoulos focused on the mathematical construction of these squares, detailing methods for creating them, particularly those of odd orders.
Luca Pacioli: Renaissance Enthusiast of Mathematical Puzzles
In the 15th century, Italian mathematician Luca Pacioli delved into the study of magic squares. A contemporary of Leonardo da Vinci, Pacioli compiled numerous examples of magic squares, reflecting the Renaissance era's fascination with mathematics and its aesthetic applications.
Heinrich Cornelius Agrippa: Bridging Mathematics and Mysticism
By the early 16th century, Heinrich Cornelius Agrippa of Germany infused magic squares with esoteric significance in his seminal work, De Occulta Philosophia (1533). Drawing from Hermetic and Kabbalistic traditions, Agrippa associated magic squares of orders 3 to 9 with the seven classical planets, attributing to each square specific mystical properties and uses in talismanic magic.
Planetary Magic Squares: The Kameas
Agrippa's planetary magic squares, known as Kameas, align each planet with a square of a specific order:
- Saturn (3×3): Magic constant 15
- Jupiter (4×4): Magic constant 34
- Mars (5×5): Magic constant 65
- Sun (6×6): Magic constant 111
- Venus (7×7): Magic constant 175
- Mercury (8×8): Magic constant 260
- Moon (9×9): Magic constant 369
Practitioners would convert names into numerical values based on alphabetic correspondences and trace paths through these squares to create sigils - symbols believed to harness planetary energies for magical purposes.
The Sator Square: A Palindromic Enigma
Distinct from numerical magic squares, the Sator Square is a word square featuring a five-word Latin palindrome:
| S | A | T | O | R |
| A | R | E | P | O |
| T | E | N | E | T |
| O | P | E | R | A |
| R | O | T | A | S |

A Sator Square, etched onto a wall in the medieval fortress town of Oppède-le-Vieux, France (source: commons.wikimedia.org)
This square has been discovered in archaeological sites dating back to the 1st century CE, including Pompeii. Throughout medieval Europe, it was revered as a protective charm, believed to ward off evil and bring good fortune.
Magic Squares in European Occult Practices
Beyond their mathematical intrigue, magic squares permeated European occult traditions. Grimoires like the Key of Solomon and The Book of the Sacred Magic of Abramelin the Mage featured magic squares intended for various purposes - from invoking spirits to securing protection. These squares often combined numerical patterns with linguistic elements, reflecting a synthesis of mathematical structure and mystical belief.
Further reading and references:
- Moschopoulos, M. On Magic Squares. Translated in Sourcebook in the Mathematics of Medieval Europe and North Africa.
- Swaney, M. "Mark Swaney on the History of Magic Squares." Arthur Magazine.
- Public Domain Review. "Marked by Stars: Agrippa's Occult Philosophy".
- Scribd. "Kameas - Magic Squares of Planetary Magic".
- Britannica. "Sator Square | Definition, History, Origin, & Facts".
Albrecht Dürer’s Magic Square: Art, Mathematics and Hidden Meaning
One of the most iconic examples of a magic square in Western art appears in Albrecht Dürer’s 1514 engraving Melencolia I. This 4×4 grid of numbers - widely known as Dürer’s Magic Square - is more than a mathematical curiosity; it is a symbolic and artistic statement that reflects Renaissance interests in numerology, harmony, and the human condition.

Detail from Melencolia I showing a 4 × 4 associative square (source: commons.wikimedia.org)
A Historical First in European Art
Dürer’s magic square is often credited as the first magic square featured in European artwork. While magic squares had appeared centuries earlier in Chinese, Indian, and Islamic contexts, Dürer’s engraving introduced the concept to the European visual tradition. His version bears a striking resemblance to the Chinese mathematician Yang Hui’s 4×4 square from the 13th century, highlighting the global legacy of this mathematical construct.
Structure and Symmetry of the Square
The square itself is a normal order-4 magic square, meaning it uses the integers from 1 to 16 with a magic constant of 34 (the sum of each row, column, and diagonal):
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
However, Dürer's square is far more intricate than a standard magic square. The sum 34 appears not only in the usual rows, columns, and diagonals, but also in:
- Each of the four quadrants (2×2 subgrids),
- The central 2×2 square: 10 + 11 + 6 + 7,
- The corner 2×2 square: 16 + 3 + 4 + 15,
- The four central numbers of each edge, when added in both clockwise (3 + 8 + 14 + 9) and counterclockwise directions (3 + 5 + 12 + 14),
- Two symmetrical quartets: (2 + 8 + 9 + 15) and (3 + 5 + 12 + 14),
-
Several cross- or kite-shaped patterns, including:
- 3 + 5 + 11 + 15
- 2 + 10 + 8 + 14
- 3 + 9 + 7 + 15
- 2 + 6 + 12 + 14
This level of layered symmetry and numerological elegance demonstrates the influence of both mathematical sophistication and esoteric symbolism.
Hidden Messages and Date Encoding
Perhaps the most famous feature of the square lies in the bottom row:
4 15 14 1
- The central two numbers, 15 and 14, clearly represent the year 1514, the date Dürer completed the engraving.
- The numbers 1 and 4 on either side correspond to the letters A and D, the artist’s initials (Albrecht Dürer) when converted via alphabetic substitution (A=1, B=2, ..., D=4).
These subtle insertions suggest Dürer used the magic square as a signature device, blending identity and date into the aesthetic matrix.
From Square to Cube
Modern researchers have noted that Dürer’s square can be extended into a 3-dimensional magic cube, preserving the same principles of balanced summation across all axes and diagonals. While Dürer himself made no documented claim to this extension, the potential 3D extrapolation of his square enhances its mathematical prestige.
Cultural Resonance: From Renaissance to Fiction
Dürer’s Melencolia I has had a profound influence on both art history and pop culture. The engraving and its embedded square play a symbolic role in Dan Brown’s 2009 novel The Lost Symbol, where they serve as keys to hidden knowledge and ancient mysteries.
In the broader context, Dürer’s use of a magic square underscores the Renaissance ideal of the "artist as intellectual" - someone who engages simultaneously in geometry, numerology, symbolism, and humanistic philosophy.
Further reading and references:
- Dürer, Albrecht. Melencolia I. Engraving, 1514.
- Swetz, Frank J. Legacy of the Luoshu: The 4,000 Year Search for the Meaning of the Magic Square. A K Peters, 2008.
- Yang Hui. Xiangjie Jiuzhang Suanfa (Commentary on the Nine Chapters on the Mathematical Art), c. 1275.
- Ifrah, Georges. The Universal History of Numbers. Wiley, 2000.
- Brown, Dan. The Lost Symbol. Doubleday, 2009.
The Sagrada Família Magic Square: Symbolism and Subversion in Sacred Geometry
One of the most intriguing intersections of modern architecture, religious symbolism, and mathematical design can be found on the Passion Façade of the Sagrada Família basilica in Barcelona. This façade, sculpted by Josep Subirachs in the late 20th century as part of Antoni Gaudí’s ongoing architectural masterpiece, features a 4×4 magic square prominently engraved in stone - a bold mathematical motif in a sacred context.

A magic square on the Sagrada Família church façade (source: commons.wikimedia.org)
A Symbolic Magic Constant
The Sagrada Família square has a magic constant of 33, representing the age of Jesus Christ at the time of the Passion. This deliberate choice ties the numerical harmony of the square to a central theological symbol of Christian belief.
Here is the magic square as it appears on the basilica’s wall:
| 1 | 14 | 14 | 4 |
| 11 | 7 | 6 | 9 |
| 8 | 10 | 10 | 5 |
| 13 | 2 | 3 | 15 |
Mathematical Structure and Deviations
At first glance, the square resembles the famous Dürer magic square from Melencolia I, which has a magic constant of 34. Indeed, the Sagrada Família square appears to be a variation of that structure, modified to yield a total of 33 for each row, column, and diagonal. This was achieved by reducing four of the numbers by 1, introducing subtle distortions to preserve the symbolic meaning while sacrificing strict mathematical purity.
However, this square is not a "normal" magic square as defined in mathematical terms. A normal 4×4 magic square must use all integers from 1 to 16 exactly once. In contrast:
- The numbers 10 and 14 appear twice.
- The numbers 12 and 16 are absent.
This makes it a symbolic or artistic magic square rather than a mathematically complete one, reflecting a creative compromise between religious meaning and numerical symmetry.
Comparison to Dürer's Square
Both Dürer’s and Subirachs’ magic squares:
- Are order-4 (4 rows and 4 columns),
- Share similar numerical arrangements and summation paths,
- Appear in symbolic visual artworks embedded in broader iconographic programs,
- Have been interpreted as containing hidden codes or messages related to faith, identity, or cosmology.
Yet while Dürer preserved the full set of numbers from 1 to 16 and embedded the date and his initials in the design, Subirachs prioritized Christian numerology, aligning the square’s logic with theological intent.
Potential for Dimensional Expansion
ike its Renaissance predecessor, the Sagrada Família square has been shown to allow extension into a 3D magic cube, where numbers in a 4×4×4 grid also add up to the same constant along each axis. This further connects the artistic representation to mathematical possibilities, even if such an extension is theoretical rather than physically represented in the church.
Symbolism in Stone
Josep Subirachs’ use of the magic square on the Passion Façade aligns with the overarching architectural and theological themes of the Sagrada Família, where symbolism pervades every surface. The Passion Façade, dedicated to the suffering and death of Christ, is minimalist, stark, and geometric - qualities echoed in the cold logic of the magic square, softened only by its theological interpretation.
Conclusion
The Sagrada Família magic square is a unique blend of sacred numerology and mathematical form, tailored to resonate with religious meaning rather than strict numerical orthodoxy. It stands as a testament to how mathematics and spirituality can merge in architectural storytelling, and how even a grid of numbers can convey profound meaning when carved into stone.
Further reading and references:
- Subirachs, Josep. Passion Façade Sculpture. Sagrada Família, Barcelona, completed 1980s–2005.
- Swetz, Frank J. Legacy of the Luoshu: The 4,000 Year Search for the Meaning of the Magic Square. A K Peters, 2008.
- Martínez, José A. "Symbolism and Geometry in the Sagrada Família." Revista de Arquitectura Religiosa, 2017.